What do we want to achieve?
In this series, we will deal with the subject of Functional Reactive with Core Java. This means that we will examine the areas of functional programming and reactive systems one by one more closely. There are already a lot of systems and libraries, which cover this topic fully and completely.
Firstly, there are approaches that deal exclusively with the functional aspects. (with this, I do not mean the development of new languages) and secondly there are the purely reactive approaches. Mostly, these approaches/frameworks are very well developed and, therefore, very powerful and comprehensive.
To start with, we will deal with the functional aspects and then combine these with the reactive ones. The aim in doing so is to illustrate the underlying thought and to offer minimalistic solutions based on the JDK.
In addition to the source text examples given in this article, I will also use the sources from the Open Source project
Functional-Reactive. The sources are available at https://github.com/functional-reactive/functional-reactive-lib
When is something object-oriented and when is it functional?
Right at the beginning, therefore, the most important question arises. When do we call something as object-oriented and when do we call it functional? This question can take quite some time to answer, if we take Java as the basis. Let’s start with some examples.
Starting with 8, there are the FunctionalInterfaces. These are used together with the lambdas. To be able to use lambdas, one must have a FunctionalInterface as target
. So, let us assume that we have a CalculationService.
We are developingfor example a web application for children, with the help of which we will present and evaluate math problems.
Therefore, our CalculationService must be in a position to present math problems and to check, whether the user has calculated the result correctly. Let us start here with a simple definition and have a look at the related screenshot.
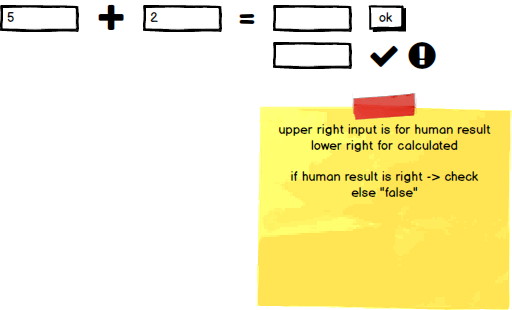
For the first draft, we need here a method, which gives us a problem and a result. Thus, we expect three values, which are related. Let us name this class as MathTask. This could look like as follows.
Source texts: v001
public class MathTask {
private int first;
private int second;
private int result;
public MathTask(int first , int second , int result) {
this.first = first;
this.second = second;
this.result = result;
}
@Override
public String toString() {
return "MathTask{" +
"first=" + first +
", second=" + second +
", result=" + result +
'}';
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (! (o instanceof MathTask)) return false;
MathTask mathTask = (MathTask) o;
if (first != mathTask.first) return false;
if (second != mathTask.second) return false;
return result == mathTask.result;
}
@Override
public int hashCode() {
int result1 = first;
result1 = 31 * result1 + second;
result1 = 31 * result1 + result;
return result1;
}
public int getFirst() {
return first;
}
public int getSecond() {
return second;
}
public int getResult() {
return result;
}
}This is a lot of source code for getting just three values. Note that there are no set methods for the attributes. But let us go further. The method, which gives this result, could look very simple in the first draft. public MathTask nextMathTask() Till now, everything is purely object-oriented. Really? Let us say at this time, yes, it is object-oriented.
public class MathService {
public MathTask nextMathTask() {
int first = 0;
int second = 0;
// create task values...
return new MathTask(first , second , (first + second));
}
}So now we have everything together for creating a problem. How does the result look now? Here, we either want to compare the result transiently with the result given by the user and then give a feedback whether it is the same, or process further the result (the comparison). For instance, if we want to save, in order to do an evaluation later, then we also need the result entered by the user.
We can now proceed in two ways. The first one is to keep the result entered by the user additionally in the object i.e., in the instance of the class MathTask. This implies that we modify the state of this instance. The second solution is to generate another class, which contains the result entered by the user and also the related problem. The reader might also want to make use of a third version. The often quoted solution is that the class MathTask gets the attribute humanResult. When the result is present, one more instance of the class MathTask is generated and then the value is set in addition to the values already known from the first step. The first instance is then not modified and rejected.
I will leave out this solution, because (in my opinion) this is a hybrid solution, and will not discuss it any further.
The subject of unchangeability (immutability) is a part of the functional approach. But it can also be used equally well in the object-oriented world. I will decide here for the second solution and generate a further class MathTaskResult with the attributes mathTask of the type MathTask and one more attribute humanResult of the type int.
public class MathTaskResult {
private MathTask mathTask;
private int humanResult;
public MathTaskResult(MathTask mathTask , int humanResult) {
this.mathTask = mathTask;
this.humanResult = humanResult;
}
public MathTask getMathTask() {
return mathTask;
}
public int getHumanResult() {
return humanResult;
}
//SNIPP toString / hashcode / equals ..
}We now have both the values, but where will the comparison be done to find out whether both the values (the one from the user and the calculated value) are the same. That is, whether the problem has been solved correctly?
This output is certainly trivial since it deals only with a comparison. But where exactly does this comparison belong?
In the UI, one can respond to the input of the user and then give a visual effect, which depicts the comparison. But is this a part of the UI? Or is the result of the comparison an attribute of the class MathTaskResult? Or is the result a method of MathService? In no case is it a part of the UI, since this is a logical operation. Only the graphical representation of the result (Yes/No) is part of the UI. The question now arises, whether it becomes a part of the class MathTaskResult or MathService.
In the object-oriented method, I would locate it in the class MathTaskResult. There, the solution would look like such that the Boolean value would be calculated on the fly. Even when one would consider saving the result, it would rather be a value to be calculated than a persistent attribute.
Therefore, we extract the validation in a method of MathService. public boolean validate(MathTaskResult result);
first refactoring - data holder
Source texts: v002
If one now wants to formulate a little more abstract, then we not only have the integer values, which we formulate in the form of a problem. We will also not just want to create a simple addition. If we wish to target the four basic operations as the first implementation for our MathService, we can modify, for instance, the example of our math problem as follows. Firstly, we describe in a generic way a triplet at the value of a random type. We name this class also as Triple.
public class Triple<T1, T2, T3>; {
private T1 t1;
private T2 t2;
private T3 t3;
public Triple(final T1 t1, final T2 t2, final T3 t3) {
this.t1 = t1;
this.t2 = t2;
this.t3 = t3;
}
public T3 getT3() {
return t3;
}
public T1 getT1() {
return t1;
}
public T2 getT2() {
return t2;
}
//SNIP hashcode / equals / toString..
}We only want to keep the three values together, whose type we still have not defined exactly. At runtime, however, we want to achieve type safety. Similarly, we can formulate this generically with our MathTaskResult.
public class Pair<T1, T2> {
private T1 t1;
private T2 t2;
public Pair(final T1 t1, final T2 t2) {
this.t1 = t1;
this.t2 = t2;
}
public T1 getT1() {
return t1;
}
public T2 getT2() {
return t2;
}
//SNIP hashcode / equals / toString..
}We have lost the expressive attribute names at this point. But we can regain these with a little effort.
public class MathTask extends Triple<Integer, Integer, Integer> {
public MathTask(Integer first , Integer second , Integer result) {
super(first , second , result);
}
public int getFirst() {
return getT1();
}
public int getSecond() {
return getT2();
}
public int getResult() {
return getT3();
}
@Override //optional
public String toString() {
return "MathTask{" +
"first=" + getT1() +
", second=" + getT2() +
", result=" + getT3() +
'}';
}
}We proceed in the same way with the class MathTaskResult.
public class MathTaskResult extends Pair<MathTask, Integer> {
public MathTaskResult(MathTask mathTask , Integer integer) {
super(mathTask , integer);
}
public MathTask getMathTask() {
return getT1();
}
public int getHumanResult() {
return getT2();
}
@Override //optional
public String toString() {
return "MathTaskResult{" +
"mathTask=" + getT1() +
", humanResult=" + getT2() +
'}';
}
}We have now extracted the generic part of the data holder and have received references to functional semantics for use in the functional logic.
Let us now look at MathService.
second refactoring - MathService
Source texts: v003
We will now deal with MathService. We have had here two methods till now. First one for generating a problem and the second for verifying, whether the problem has been solved correctly.
Let us discuss at first the generation of problem. If one is solving the first math problems with children, one then starts, for instance, in the range zero to ten. This means that we have different requirements for the task.
- The result may not be greater than 10.
- The result may not be less than 0.
- 0 may not be present as the result
- None of the parameters may be 0. (but can be later ;-))
- the same problem may not be presented again successively
These are quite a lot of requirements to be taken into consideration. If one now takes into account all basic calculation operations, then further specific requirements are added. For instance, in case of division, only integer values should be considered. And many more, of which one suddenly becomes aware, when the child uses the application for the first time. I will be intentionally omitting here the possible validations during the input.
First, let us have a look at the addition. This basic operation itself as selection option is not a parameter of the method for generating the next problem.
An initial implementation, thus, could be as follows.
public class MathService {
public MathTask nextMathTask(int paramBoundFirst , int paramBoundSecond) {
final Random random = new Random(System.nanoTime());
int first = random.nextInt(paramBoundFirst);
int second = random.nextInt(paramBoundSecond);
return new MathTask(first , second , (first + second));
}
public boolean validate(MathTaskResult mathTaskResult){
return mathTaskResult.getHumanResult() ==
mathTaskResult.getMathTask().getResult();
}
}The question now arises, whether we really need an instance of a class for both these methods. Each method is called once, without there being a state, which must remain intact over more than one method call. This too is an attribute of functional programming. That is, the statelessness itself. A state may be retained only within a method for so long, till the method terminates. How does this now look like, when we extract this further so that we do not have to hold an instance of the class MathService. This itself represents a state .
Let us first shift everything to an interface so that even by mistake an attribute does not arise at the class level of the class MathService with time. An interface and the methods themselves are defined static from the class.
Source texts: v004
public interface MathService {
public static MathTask nextMathTask(int paramBoundFirst , int paramBoundSecond) {
final Random random = new Random(System.nanoTime());
int first = random.nextInt(paramBoundFirst);
int second = random.nextInt(paramBoundSecond);
return new MathTask(first , second , (first + second));
}
public static boolean validate(MathTaskResult mathTaskResult){
return mathTaskResult.getHumanResult() ==
mathTaskResult.getMathTask().getResult();
}
}With this, the source text gets reduced to the following when used.
public class Main {
public static void main(String[] args) {
final MathTask mathTask = MathService.nextMathTask(5,5);
int humanResult = 0;
MathTaskResult mathTaskResult = new MathTaskResult(mathTask , humanResult);
boolean validate = MathService.validate(mathTaskResult);
System.out.println("mathTask = " + mathTask);
System.out.println("mathTaskResult = " + mathTaskResult);
System.out.println("validate = " + validate);
}
}Now only static imports and we get:
public class Main {
public static void main(String[] args) {
final MathTask mathTask = nextMathTask(5,5);
int humanResult = 0;
MathTaskResult mathTaskResult = new MathTaskResult(mathTask , humanResult);
boolean validate = validate(mathTaskResult);
System.out.println("mathTask = " + mathTask);
System.out.println("mathTaskResult = " + mathTaskResult);
System.out.println("validate = " + validate);
}
}We now have two static methods in an interface without holding object reference. If we now look at the implementation, we can correct one thing very easily. Till now it has been assumed that the result may not exceed the value 10 and that the input values themselves may not exceed five.
In order to make it easier for the user of the method, we will now change the signature. Now only the maximum result value will be specified. The method then itself determines the values for the respective parameters internally. We thus get the encapsulation in the form that we need to know less about the internal functions of the method.
public static MathTask nextMathTask(int maxResultValue) {
final Random random = new Random(System.nanoTime());
int bound = maxResultValue / 2;
int first = random.nextInt(bound);
int second = random.nextInt(bound);
return new MathTask(first , second , (first + second));
}What we now have is a transformation from the maximum result value to an instance of the class MathTask. We can also formulate this as follows. Function<Integer,MathTask> with the condition that the integer may not be greater than the maximum result value. And do not forget, it should also become negative and…
But we will now first write this as function. Since Java 8, there is here the FunctionalInterface Function<A,B>.
public static Function<Integer, MathTask> mathTask = new Function<Integer, MathTask>() {
@Override
public MathTask apply(Integer maxResultValue) {
final Random random = new Random(System.nanoTime());
int bound = maxResultValue / 2;
int first = random.nextInt(bound);
int second = random.nextInt(bound);
return new MathTask(first , second , (first + second));
}
};This is now here the conventional way of writing. Thanks to the new syntax, we can write this in a more compact way.
public static Function<Integer, MathTask> mathTask = (maxResultValue) -> {
final Random random = new Random(System.nanoTime());
int bound = maxResultValue / 2;
int first = random.nextInt(bound);
int second = random.nextInt(bound);
return new MathTask(first , second , (first + second));
};Are we now doing functional programming? In my opinion, this is still not functional in the real sense, but we are coming closer to it and are more and more paying attention to functional aspects.
Till now, we have tried to formulate the functions directly. But actually one still wants to have an instance. Where to get this from? Let us rewrite the last example once again in a way that one gets a function as the return value.
Source texts: v006
public static Function<Integer, MathTask> mathTaskFunction() {
return (maxResultValue) -> {
final Random random = new Random(System.nanoTime());
int bound = maxResultValue / 2;
int first = random.nextInt(bound);
int second = random.nextInt(bound);
return new MathTask(first , second , (first + second));
};
}We now have a method, which returns an instance of a function, with which we can work freely, because we are sure that this instance will be used only by us. We can now implement the same with the method validate.
static Function<MathTaskResult, Boolean> validate(){
return (mathTaskResult) -> mathTaskResult.getHumanResult() ==
mathTaskResult.getMathTask().getResult();
}How does now the related source text look like in usage?
int maxResultValue = 10;
int humanResult = 0;
final Function<Integer, MathTask> mathTaskFunction = MathService.mathTaskFunction();
final MathTask mathTask = mathTaskFunction.apply(maxResultValue);
final BiFunction<Integer, MathTask, MathTaskResult> resultBiFkt
= (result , task) -> new MathTaskResult(task , result);
final MathTaskResult mathTaskResult = resultBiFkt.apply(humanResult , mathTask);
final Function<MathTaskResult, Boolean> validate = MathService.validate();
final Boolean apply = validate.apply(mathTaskResult);
I have also defined one more function at the respective places. This helps in transforming MathTask and the result from the user humanResult to an instance of the type MathTaskResult.
But what is the benefit of these functions? In each case, it is certain that with functions one can no longer solve problems than with object-oriented Java. Therefore, one must look for the benefits at some other place.
Let us start with rewriting the available one a bit.
final BiFunction<Integer, MathTask, MathTaskResult> resultBiFkt
= (result , task) -> new MathTaskResult(task , result);
Boolean result = resultBiFkt
.andThen(validate())
.apply(humanResult , mathTaskFunction().apply(maxResultValue));
We have now used here a property of the functions. This implies here the combination of functions by means of andThen. Using this, the functions are attached one after the other. The result of the previous function is the input for the next function. The result is again a function. Function<A, B> andThen Function<B,C> becomes Function<A, C>
We will now use here a BiFunction i.e., a function, which has two input parameters and one output parameter. One can combine these also by means of andThen to make one simple function. But what to do, if we wish to design it a little symmetrical? We can quickly get rid of this BiFunction by putting together both the input parameters again in a Pair.
final Function<Integer, Pair<MathTask, Integer>> integerPairFunction = mathTaskFunction()
.andThen(mathTask -> new Pair<>(mathTask , humanResult));
final Function<Pair<MathTask, Integer>, MathTaskResult> mapToMathTaskResult
= (resultPair) -> new MathTaskResult(resultPair.getT1() , resultPair.getT2());
Boolean aBoolean = integerPairFunction
.andThen(mapToMathTaskResult)
.andThen(validate())
.apply(maxResultValue);We have now gotten rid of BiFunction. However, this solution should not be used, since we are using the variable humanResult in the function itself. This should rather be an input parameter. Secondly, interactions with the user are necessary between the transactions. The values from the instance MathTask must also be shown in the UI. To cut a long story short, we must split this again in two sections.
//t1 - show the values on Screen
final MathTask mathTask = mathTaskFunction().apply(maxResultValue);
final Function<Pair<MathTask, Integer>, MathTaskResult> mapToMathTaskResult
= (resultPair) -> new MathTaskResult(resultPair.getT1() , resultPair.getT2());
//t2 - button was pressed
final Boolean aBoolean = mapToMathTaskResult //t2 - button was pressed
.andThen(validate())
.apply(new Pair<>(mathTask , humanResult));
Source texts: v007
The transformation can still be extracted in the method public stativ Function<Pair<MathTask, Integer>, MathTaskResult> mapToMathTaskResul()
//t1 - show the values on Screen
final MathTask mathTask = mathTaskFunction().apply(maxResultValue);
//t2 - button was pressed
final Boolean aBoolean = mapToMathTaskResult().andThen(validate()).apply(new Pair<>(mathTask , humanResult)
One can also combine the functions with each other using compose(..). The sequence here is exactly the opposite of andThen(..). This gives us another possibility of formulating the last statement.
//t1 - show the values on Screen
final MathTask mathTask = mathTaskFunction().apply(maxResultValue);
//t2 - button was pressed
final Boolean aBoolean = validate().compose(mapToMathTaskResult()).apply(new Pair<>(mathTask , humanResult));
Summary
What have we achieved till now? We have modified a bit of the existing source text and tested out initial ideas and approaches of functional programming. We have intentionally not taken the formal path and till now also not clearly defined, when we refer to object-oriented and when to functional programming.
We will work on it further in the next sections and deal with integration in the existing (legacy) source text as well as also with the creation of new projects / modules .
You can find the source code at:
https://github.com/Java-Publications/functional-reactive-with-core-java-001.git
If you have questions or comments, simply contact me at sven@vaadin.com or via Twitter @SvenRuppert.
Happy coding!